
皮克公式
皮克公式定理是一种计算格点点阵中多边形面积的方法,公式如下:
S = B ÷ 2 + A - 1
公式中:
S:多边形的面积
B:多边形边上的点的数量
A:多边形内部的点的数量
通俗地描述为:格点多边形图形面积 = 多边形边上的点之和÷2 + 多边形内部的点之和 - 1
皮克定理公式是1899年奥地利数学家皮克(Georg Alexander Pick)发现的,“皮克定理”(Pick's Theorem)被誉为“有史以来最重要的100个数学定理之一”。
皮克定理是这样描述的:给定顶点座标均是整点(或正方形格子点)的简单多边形,即多边形的顶点都是格点点阵中的点,计算点阵中多边形面积的公式:S=a+b÷2-1
其中a表示多边形内部的点数,b表示多边形边界上的点数,S表示多边形的面积。
皮克公式例题
某地区小学五年级(上)数学期末试卷中的一道图形计算题,要求在格点的点阵中连线画三角形,并计算这个三角形的面积,如果知道皮克定理公式可以很方便计算出答案。
图形计算(共6分)
下图中,每相邻两个点之间的距离为1cm。
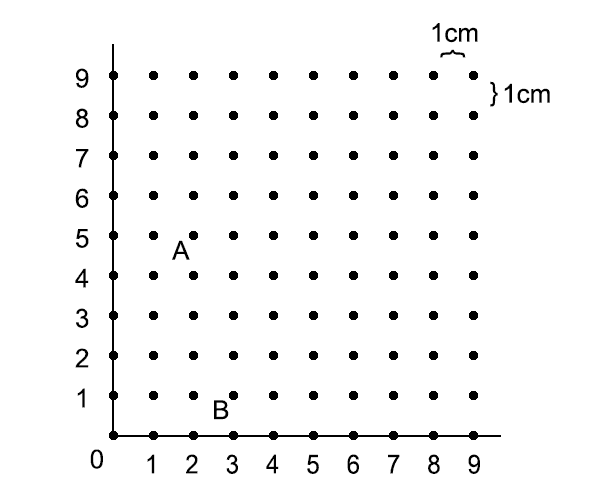
1、图中A点用数对表示是( , ),B点用数对表示是( , )。C点的位置是(8,7),请在图中标出C点。(3分)
2、将点A、B、C依次连接成三角形。(1分)
3、这个三角形的面积是多少平方厘米?(2分)
分析:第1和第2小题很简单,只要在图上数点就可以得出A(2,5),B(3,1),而第3小题要计算三角形ABC的面积,满足皮克定理的条件,正方形格子点,这时如果使用皮克定理就可以很简单得出答案。
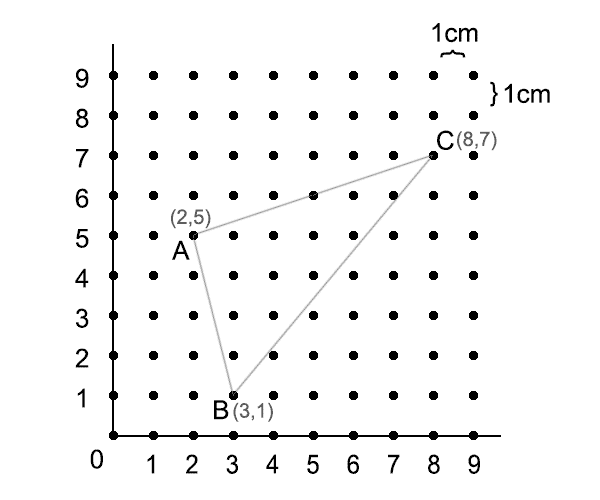
通过连线可以得出三角形ABC,其中三角形边上的点数B=4,三角形内部的点数A=12,应用皮克定理 S = B ÷ 2 + A -1 = 4 ÷ 2 + 12 - 1 = 13 cm2
由此可得第3小题中三角形ABC的面积是13平方厘米。
皮克公式验证
如果不知道皮克定理,其实也可以通过计算得出三角形的面积,分析如下图:
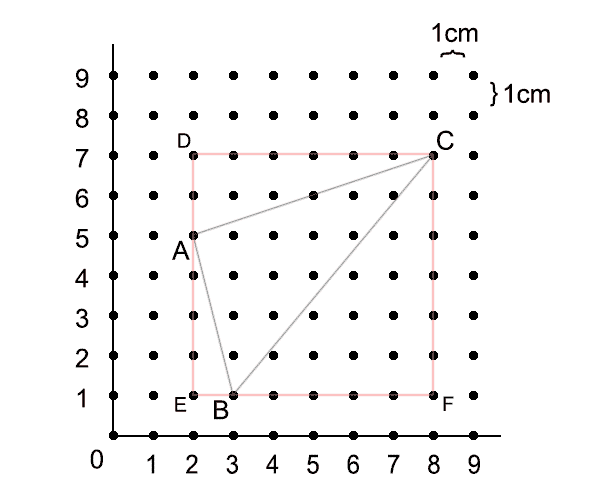
由上图可知,三角形ABC的面积等于正方形DEFC的面积减去三角形CDA、三角形AEB和三角形BFC的面积之和,而这三个三角形的面积可以很简单地通过数格点的方法读出。
三角形ABC的面积 = 正方形DEFC的面积 - 三角形CDA的面积 - 三角形AEB的面积 - 三角形BFC的面积 = 36 - 6 - 2 - 15 = 13 cm2
可以看到,通过画辅助图形计算出的三角形面积和使用皮克定理公式计算出的结果是一致的。
当然,不止三角形,在格点点阵连线的任意顶点是格点的多边形面积都可以使用皮克定理公式计算。
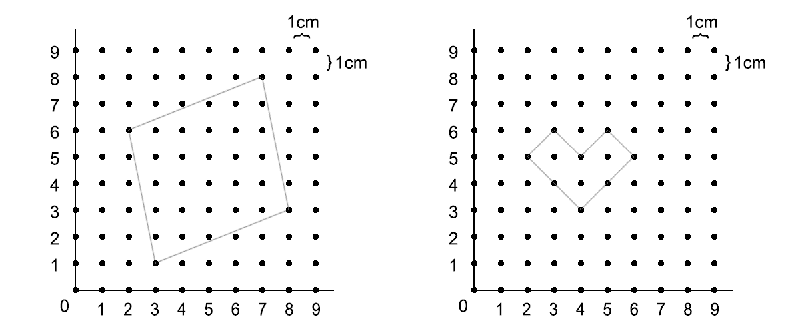
上图两个多边形的面积计算如下:
S1 = 4 / 2 + 26 - 1 = 27
S2 = 8 / 2 + 3 - 1 = 6
验证的方法同上,可以通过各个顶点画长方形或正方形,然后利用长方形或正方形的面积减去多个三角形的面积即可得出格点多边形的面积,此处不再详细计算,有兴趣的朋友可以自行尝试一下。
总结
使用皮克定理公式可以很简易地计算出格点连线多边形的面积,但是如果格点多边形需要自己画,如上面的例题,建议使用画方形的方法减去多边形外围的三角形面积得出多边形的面积,为防止手工画图时不准确导致边上的点或多边形内部的点出现误差,如此一来可能导致最后计算结果出错。
如果题目已经给出图形,可以直接使用皮克定理的公式计算,比较方便。